| |||||||||
|
|
|||||||||
| Splay (Kink) Angle Distribution | |||||||||
|
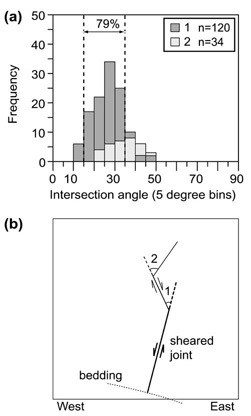
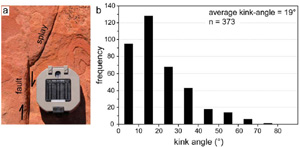
Splay or kink angle refers to the acute angle between a fault and its extension in mode-I, that is, its splay fracture(s). Splay fractures form at the extensional quadrants of a shear fracture parallel to the local greatest compressive stress. Therefore, kink angles depend on the orientation between the faults and the local principal stresses, and consequently, the angle between the shear fracture and the greatest remote compressive stress, as well as the friction coefficient on the sliding plane. Davatzes and Aydin (2003) reported kink angles between 10° and 50° (Figure 1) on several sheared joint-based normal faults developed through successive splay fracturing and shearing of the splays in sandstone along and across the Waterpocket monocline at the Capitol Reef National Park, Utah. The median kink angle between the first and second generation of splays is 28°, while the median angle between the second and third generation is 37°. They also observed that the kink angles do not correlate to fault offset, bed dip, location in the larger structure (monocline), sheared joint length, or dip angle. de Joussineau et al. (2007) measured approximately 800 kink angles associated with sheared joint-based strike-slip faults in sandstone at Valley of Fire State Park, southern Nevada. They identified two configurations of faults leading to different kink angle distributions. For single isolated fault configurations (Figure 2a), the measured kink angles are generally less than 30° with an average value of about 19° (Figure 2b).
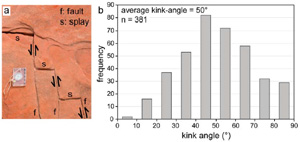
For the interacting fault configurations (Figure 3a), the kink angle distribution is significantly different than that for isolated fault cases, with most of the kink angles being greater than 40° with an average value of about 50° (Figure 3b). de Joussineau et al. (2007) analyzed this data set using isolated faults under plane strain condition and found that small kink angles correspond to smaller angles between the shear fracture and the remote maximum compressive stress, while large kink angles correspond to a greater angle between the fault and the maximum stress. Models of interacting faults show that, in addition to the critical role of the angle of the faults with the remote maximum compressive stress, fault overlap and fault separation can result in important variations in the kink angles, which could explain the variation of kink angles measured in the field at the same locality, which presumably was subjected to the remote greatest principal stress of the same orientation. These case studies in Capitol Reef National Park and Valley of Fire State Park demonstrate the role of fault interaction on the observed kink angles associated with normal and strike-slip faults, respectively, and the importance of stress states as well as the fault frictional properties.
Kink angles have also been studied experimentally and theoretically. In experiments (Brace and Bombolakis, 1963; Nemat Nasser and Horii, 1982), the kink angles between a shear fracture and its splays have been found to be influenced by the frictional properties of the sliding surfaces, the remote stress field, and the angle of the shear fracture to the maximum compressive stress. In the theoretical studies, two models have been used to investigate kink angles: a rather simpler first one is based on the classical linear elastic fracture mechanics (LEFM) and another, a more advanced model, incorporates cohesive end zone (CEZ). LEFM based models (Erdogan and Sih, 1963; Cotterell and Rice, 1980; Ingraffea, 1987) predict a kink angle equal to 70.5° using the maximum circumferential stress criterion. However, kink angles much smaller than 70.5° are reported along natural faults with a shear offset and no evidence of opening perpendicular to the faults. This discrepancy between theory and nature has been attributed to the fact that the LEFM model is associated with stress singularity and infinite displacement gradient at the fault tips, which is unrealistic because no material can bear infinite stress. To overcome this problem, a zone of higher friction or cohesion around the tips of the modeled shear fractures are introduced (Dugdale, 1960; Barenblatt, 1962). The CEZ models apparently reproduce the kink angles observed in nature (Martel, 1997; Willemse and Pollard, 1998). | |||||||||
| Reference: |
|||||||||
| Barenblatt, G.I., 1962 Brace, W.F., Bombolakis, E.G., 1963 Davatzes, N.C., Aydin, A., 2003 de Joussineau, G., Mutlu, O., Aydin, A., Pollard, D.D., 2007 Dugdale, D.S., 1960 Erdogan, F., Sih, G.C., 1963 Ingraffea, A.R., 1987 Martel, S.J., 1997 Nemat-Nasser, S., Horii, H., 1982 Willemse, E.J.M, Pollard, D.D., 1998 |
|||||||||
|
Readme | About Us | Acknowledgement | How to Cite | Terms of Use | Ⓒ Rock Fracture Knowledgebase |
|||||||||